2.3 Cyclic time granularities

Cyclic granularities represent cyclical repetitions in time. They can be thought of as additional categorizations of time that are not linear. Cyclic granularities can be constructed from two linear granularities, that relate periodically; the resulting cycles can be either regular (circular), or irregular (quasi-circular).

2.3.1 Circular granularities

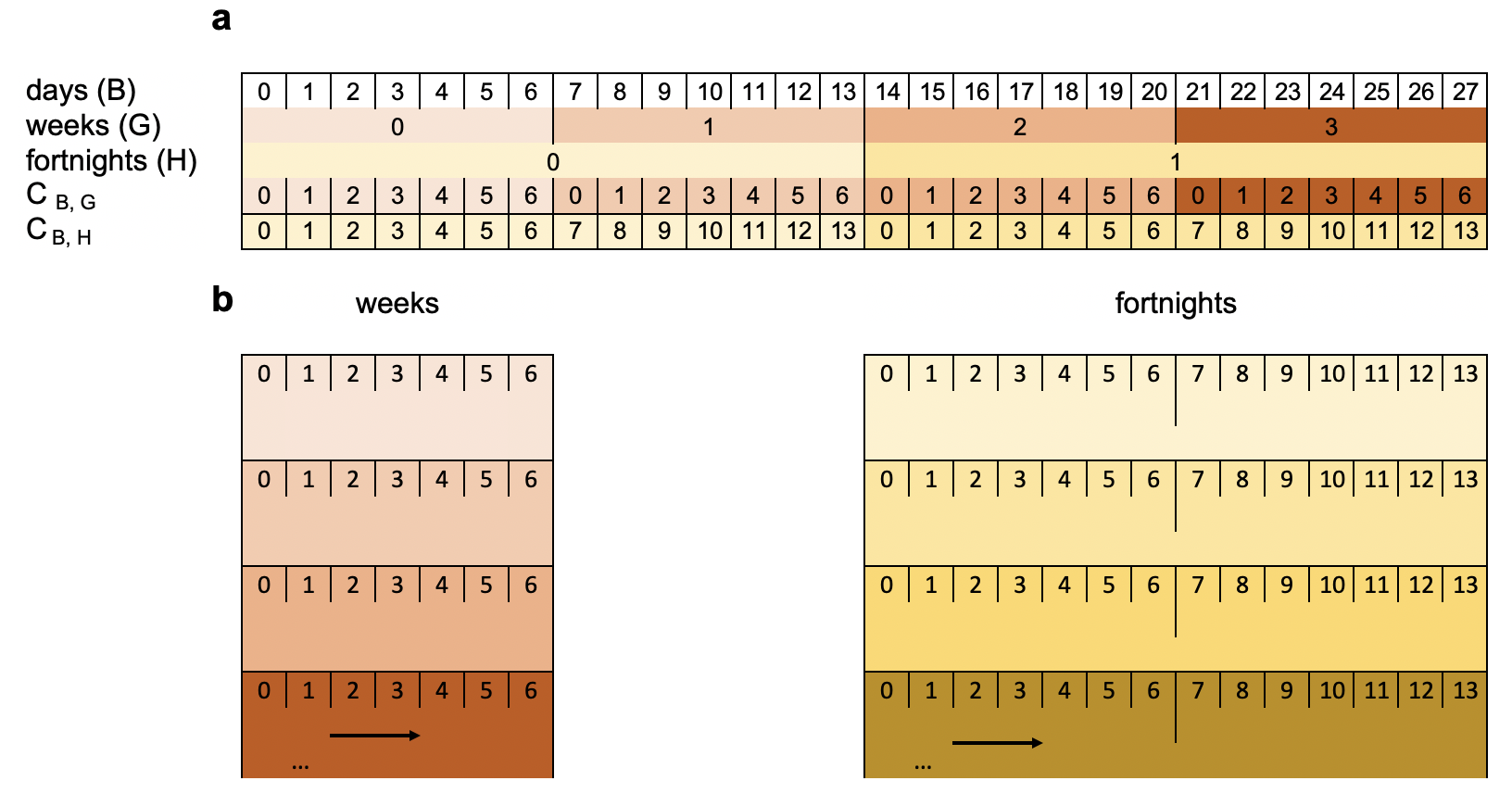
Figure 2.2: Index sets for some linear and circular granularities (a). Circular granularities can be constructed by slicing the linear granularity into pieces and stacking them (b).

illustrates some linear and cyclical granularities. Cyclical granularities are constructed by cutting the linear granularity into pieces, and stacking them to match the cycles (as shown in b). \(B, G, H\) (day, week, fortnight, respectively) are linear granularities. The circular granularity \(C_{B, G}\) (day-of-week) is constructed from \(B\) and \(G\), while circular granularity \(C_{B, H}\) (day-of-fortnight) is constructed from \(B\) and \(H\). These overlapping cyclical granularities share elements from the linear granularity. Each of \(C_{B , G}\) and \(C_{B , H}\) consist of repeated patterns \(\{0, 1, \dots, 6\}\) and \(\{0, 1, \dots, 13\}\) with \(P=7\) and \(P=14\) respectively.

Suppose \({L}\) is a label mapping that defines a unique label for each index \(\ell \in \{ 0,1,\dots, (P-1)\}\). For example, the label mapping \(L\) for \(C_{B, G}\) can be defined as \[ L: \{0,1, \dots, 6\} \longmapsto\ \{\text{Sunday}, \text{Monday}, \dots, \text{Saturday}\}. \]

In general, any circular granularity relating two linear granularities can be expressed as \[ C_{G, H}(z) = \lfloor z/P(B,G) \rfloor\mod P(G,H), \] where \(H\) is periodic with respect to \(G\) with regular mapping and period \(P(G,H)\). Table  shows several circular granularities constructed using minutes as the bottom granularity.

2.3.2 Quasi-circular granularities

A quasi-circular granularity cannot be defined using modular arithmetic because of the irregular mapping. However, they are still formed with linear granularities, one of which groups periodically into the other. shows some examples of quasi-circular granularities.

For example, day-of-year is quasi-periodic with either 365 or 366 granules of \(B\) (days) within each granule of \(G'\) (years). The pattern repeats every \(4\) years (ignoring leap seconds). Hence \(R'= 4\). \(Q_{B, G'}\) is a repetitive categorization of time, similar to circular granularities, except that the number of granules of \(B\) is not the same across different granules of \(G'\).

2.3.3 Aperiodic granularities

Aperiodic linear granularities are those that cannot be specified as a periodic repetition of a pattern of granules as described in Definition . Aperiodic cyclic granularities capture repetitions of these aperiodic linear granularities. Examples include public holidays which repeat every year, but there is no reasonably small span of time within which their behavior remains constant. A classic example is Easter (in the Western tradition) whose dates repeat only after 5.7 million years (Reingold and Dershowitz 2001). In Australia, if a standard public holiday falls on a weekend, a substitute public holiday will sometimes be observed on the first non-weekend day (usually Monday) after the weekend. Examples of aperiodic granularity may also include school holidays or a scheduled event. All of these are recurring events, but with non-periodic patterns. Consequently, \(P_i\) (as given in ) are essentially infinite for aperiodic granularities.

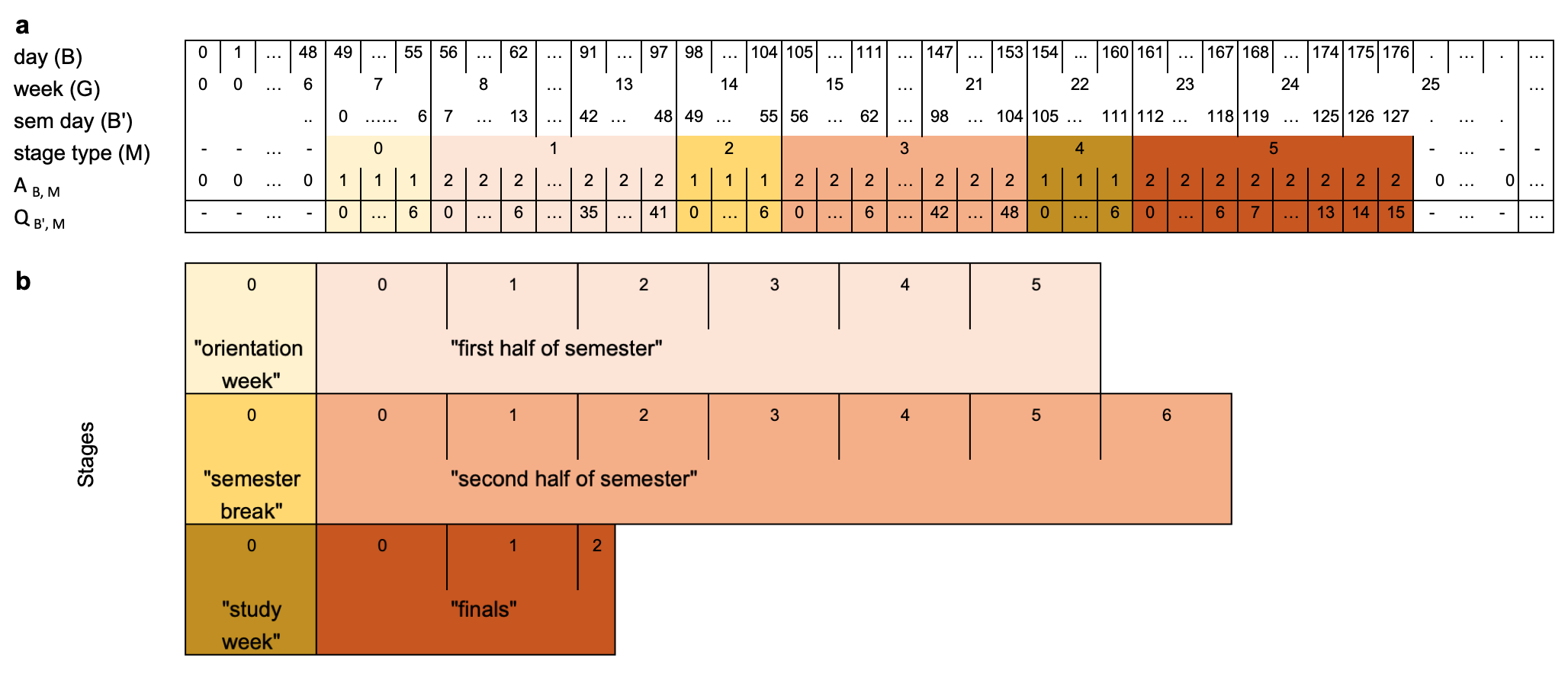
Figure 2.3: (ref:aperiodic-example)

(ref:aperiodic-example) Quasi-circular and aperiodic cyclic granularities illustrated by linear (a) and stacked-displays (b) progression of time. The linear display shows the granularities days (\(B\)), weeks (\(G\)), semester days (\(B'\)), and stages of a semester (\(M\)) indexed over a linear representation of time. The granules of \(B'\) are only defined for days when the semester is running. Here a semester spans 18 weeks and 2 days, and consists of 6 stages. It starts with a week of orientation, followed by an in-session period (6 weeks), a break (1 week), the second half of semester (7 weeks), a 1-week study break before final exams, which spans the next 16 days. This distribution of semester days remains relatively similar for every semester. \(Q_{B',M}\) with P = 128 is a quasi-circular granularity with repeating patterns, while \(A_{B,M}\) is an aperiodic cyclic granularity as the placement of the semester within a year varies from year to year with no fixed start and end dates.

For example, consider the school semester shown in . Let the linear granularities \(M_1\) and \(M_2\) denote the teaching and non-teaching stages of the semester respectively. Both \(M_1\), \(M_2\) and \(M = M_{1}\bigcup M_{2}\) denoting the “stages” of the semester are aperiodic with respect to days (\(B\)) or weeks (\(G\)). Hence \(A_{B, M}\) denoting day-of-the-stage would be an aperiodic cyclic granularity because the placement of the semester within a year would vary across years. Here, \(Q_{B', M}\) denoting semester-day-of-the-stage would be a quasi-circular granularity since the distribution of semester days within a semester is assumed to remain constant over years. Here semester-day is denoted by “sem day” (\(B'\)) and its granules are only defined for the span of the semesters.

2.3.4 Relativities

The hierarchical structure of time creates a natural nested ordering which can be used in the computation of relative pairs of granularities.

For example, shows the hierarchy table for the Mayan calendar. In the Mayan calendar, one day was referred to as a kin and the calendar was structured such that 1 kin = 1 day; 1 uinal = 20 kin; 1 tun = 18 uinal (about a year); 1 katun = 20 tun (20 years) and 1 baktun = 20 katun.

Like most calendars, the Mayan calendar used the day as the basic unit of time (Reingold and Dershowitz 2001). The structuring of larger units, weeks, months, years and cycle of years, though, varies substantially between calendars. For example, the French revolutionary calendar divided each day into 10 “hours,” each “hour” into 100 “minutes” and each “minute” into 100 “seconds,” the duration of which is 0.864 common seconds. Nevertheless, for any calendar, a hierarchy table can be defined. Note that it is not always possible to organize an aperiodic linear granularity in a hierarchy table. Hence, we assume that the hierarchy table consists of periodic linear granularities only, and that the cyclic granularity \(C_{G(\ell),G(m)}\) is either circular or quasi-circular.

In the Mayan calendar (Table @ref{tab:tab-mayan}), kin-of-tun or kin-of-baktun are examples of multiple-order-up granularities and single-order-up granularities are kin-of-uinal, uinal-of-tun etc.

2.3.5 Computation

Following the calendar algebra of Ning, Wang, and Jajodia (2002) for linear granularities, we can define cyclic calendar algebra to compute cyclic granularities. Cyclic calendar algebra comprises two kinds of operations: (1) single-to-multiple (the calculation of multiple-order-up cyclic granularities from single-order-up cyclic granularities) and (2) multiple-to-single (the reverse).

Single-to-multiple order-up

Methods to obtain multiple-order-up granularity will depend on whether the hierarchy consists of all circular single-order-up granularities or a mix of circular and quasi-circular single-order-up granularities. Circular single-order-up granularities can be used recursively to obtain a multiple-order-up circular granularity using \[\begin{equation} \label{eq:eq7} C_{G_\ell,G_m}(z) = \sum_{i=0}^{m - \ell - 1} P(\ell, \ell+i)C_{G_{\ell+i},G_{\ell+i+1}}(z), \end{equation}\] where \(\ell < m - 1\) and \(P(i, i) = 1\) for \(i=0,1,\dots,m-\ell-1\), and \(C_{B, G}(z) = z\mod P(B, G)\) as per Equation .

For example, the multiple-order-up granularity \(C_{\text{uinal},\text{katun}}\) for the Mayan calendar could be obtained using \[\begin{align*} C_{\text{uinal}, \text{baktun}}(z) &= C_{\text{uinal}, \text{tun}}(z) + P(\text{uinal}, \text{tun})C_{\text{tun},\text{katun}}(z) + P(\text{uinal},\text{katun})C_{\text{katun}, \text{baktun}}(z) \\ &= C_{\text{uinal}, \text{tun}}(z) + 18 \times{ C_{\text{tun},\text{katun}}(z)} + 18 \times 20 \times{C_{\text{katun}, \text{baktun}}(z)} \end{align*}\]

where \(z\) is the index of the bottom granularity \(kin\).

Now consider the case where there is one quasi-circular single order-up granularity in the hierarchy table while computing a multiple-order-up quasi-circular granularity. Any multiple-order-up quasi-circular granularity \(C_{\ell, m}(z)\) could then be obtained as a discrete combination of circular and quasi-circular granularities.

Depending on the order of the combination, two different approaches need to be employed leading to the following cases:

• \(C_{G_{\ell},G_{m'}}\) is circular and \(C_{G_{m'},G_{m}}\) is quasi-circular \[\begin{equation} \label{eq:multifromsingle-quasi1} C_{G_\ell,G_{m}}(z) = C_{G_{\ell},G_{m'}}(z) + P(\ell, m')C_{G_{m'},G_{m}}(z) \end{equation}\]

• \(C_{G_{\ell},G_{m'}}\) is quasi-circular and \(C_{G_{m'},G_{m}}\) is circular \[\begin{equation} \label{eq:multifromsingle-quasi2} C_{G_\ell,G_{m}}(z) = C_{G_{\ell},G_{m'}}(z) + \sum_{w=0}^{C_{G_{m'},G_{m}}(z) -1}(\vert T_{w} \vert) \end{equation}\] where \(T_w\) is such that \(G_{m'}(w) = \bigcup_{z \in T_w}G_{\ell}\) and \(\vert T_w \vert\) is the cardinality of set \(T_w\).

For example, the Gregorian calendar () has day-of-month as a single-order-up quasi-circular granularity, with the other granularities being circular. Using Equations and , we then have: \[ C_{hour, month}(z) = C_{hour, day}(z) + P(hour, day)*C_{day, month}(z) \] \[ C_{day, year}(z) = C_{day,month}(z) + \sum_{w=0}^{C_{month, year}(z)-1}(\vert T_{w} \vert), \] where \(T_w\) is such that \(month(w) = \bigcup_{z \in T_w}day(z)\).

Multiple-to-single order-up

Similar to single-to-multiple operations, multiple-to-single operations involve different approaches for all circular single-order-up granularities and a mix of circular and quasi-circular single-order-up granularities in the hierarchy. For a hierarchy table \(H_n: (G, C, K)\) with only circular single-order-up granularities and \(\ell_1, \ell_2, m_1, m_2 \in {1, 2, \dots, n}\) and \(\ell_2<\ell_1\) and \(m_2>m_1\), multiple-order-up granularities can be obtained using Equation . \[\begin{equation} \label{eq:all-circular-multiple} C_{G_{\ell_1}, G_{m_1}}(z) = \lfloor C_{G_{\ell_2}, G_{m_2}}(z)/P(\ell_2,\ell_1) \rfloor \mod P(\ell_1, m_1) \end{equation}\] For example, in the Mayan Calendar, it is possible to compute the single-order-up granularity tun-of-katun from uinal-of-baktun, since \(C_{tun, katun}(z) = \lfloor C_{uinal, baktun}(z)/18\rfloor \mod 20\).

Multiple order-up quasi-circular granularities

Single-order-up quasi-circular granularity can be obtained from multiple-order-up quasi-circular granularity and single/multiple-order-up circular granularity using Equations and .